Evaluate the following triple integral. $\int_0^2 \int_0^3 \int_0^2\ dx\ dy\ dx$

Solution

$\begin{aligned} \int_0^2 \int_0^3 \int_0^2\ dx\ dy\ dx &= \int_0^2 \int_0^3 2\ dy\ dx\ &= \int_0^2 6\ dx = \ans{12} \end{aligned}$

Note that this gives the volume of a $2×3×2$ cube.

Use a triple integral to find the volume of the prism $D$ in the first octant bounded by the planes $y=4−2x$ and $z=6$.

Solution

Note that this prism is $D={(x,y,z)\ :\ 0 \leq x \leq 2,\ 0 \leq y \leq 4-2x,\ 0 \leq z \leq 6}$ or $D={(x,y,z)\ :\ 0 \leq x \leq 2-\dfrac{1}{2}y,\ 0 \leq y \leq 4,\ 0 \leq z \leq 6}$

We can write this integral in several ways, all of which give the same answer: $\begin{aligned} V &= \int_0^6 \int_0^2 \int_0^{4-2x} \ dy\ dx\ dz\ &= \int_0^2 \int_0^{4-2x} \int_0^6 \ dx\ dy\ dx\ &= \int_0^6 \int_0^4 \int_0^{2-y/2} \ dx\ dy\ dz\ &= \ans{24} \end{aligned}$

Notice that in each case, we have to make sure that we use the limits that involve one variable before we integrate with respect to that variable.

If the density function is given by $ρ=2−z$ kg/m$^3$ for the cube $D={(x,y,z)\ :\ 0 \leq x \leq 3,\ 0 \leq y \leq 2,\ 0 \leq z \leq 1},$ find the mass of this cube.

Solution

$\begin{aligned} M &= \int_0^1 \int_0^2 \int_0^3 2-z\ dx\ dy\ dz\ &= \int_0^1 \int_0^2 6-3z\ dy\ dz\ &= \int_0^1 12-6z\ dz\ &= 12z-3z^2 \bigg|_0^1 = \ans{9\ kg} \end{aligned}$

Find the average value of $f(x,y,z)=250xy \sin(πz)$ over the cube $D={(x,y,z)\ :\ 0 \leq x \leq 2,\ 0 \leq y \leq 2,\ 0 \leq z \leq 1}.$

Solution

$\begin{aligned} \overline{f} &= \dfrac{1}{4} \int_0^1 \int_0^2 \int_0^2 250 xy \sin (\pi z) \ dx\ dy\ dz\ &= \dfrac{1}{4} \int_0^1 \int_0^2 500 y \sin (\pi z) \ dy\ dz\ &= \dfrac{1}{4} \int_0^1 1000 \sin (\pi z)\ dz\ &= \dfrac{1}{4} \bigg[ -1000 \cdot \dfrac{1}{\pi} \cos (\pi z) \bigg]_0^1\ &= \ans{\dfrac{500}{\pi}} \end{aligned}$

Evaluate $\displaystyle\iiint_D 2x\ dV$, where $D={(x,y,z)\ :\ 0 \leq y \leq 2,\ 0 \leq x \leq \sqrt{4-y^2},\ 0 \leq z \leq y}.$

Solution

$\begin{aligned} \int_0^2 \int_0^{\sqrt{4-y^2}} \int_0^y &2x\ dz\ dx\ dy\ &= \int_0^2 \int_0^{\sqrt{4-y^2}} 2xy \ dx\ dy\ &= \int_0^2 (4-y^2)y\ dy\ &= 2y-\dfrac{1}{4}y^4 \bigg|_0^2 = \ans{4} \end{aligned}$

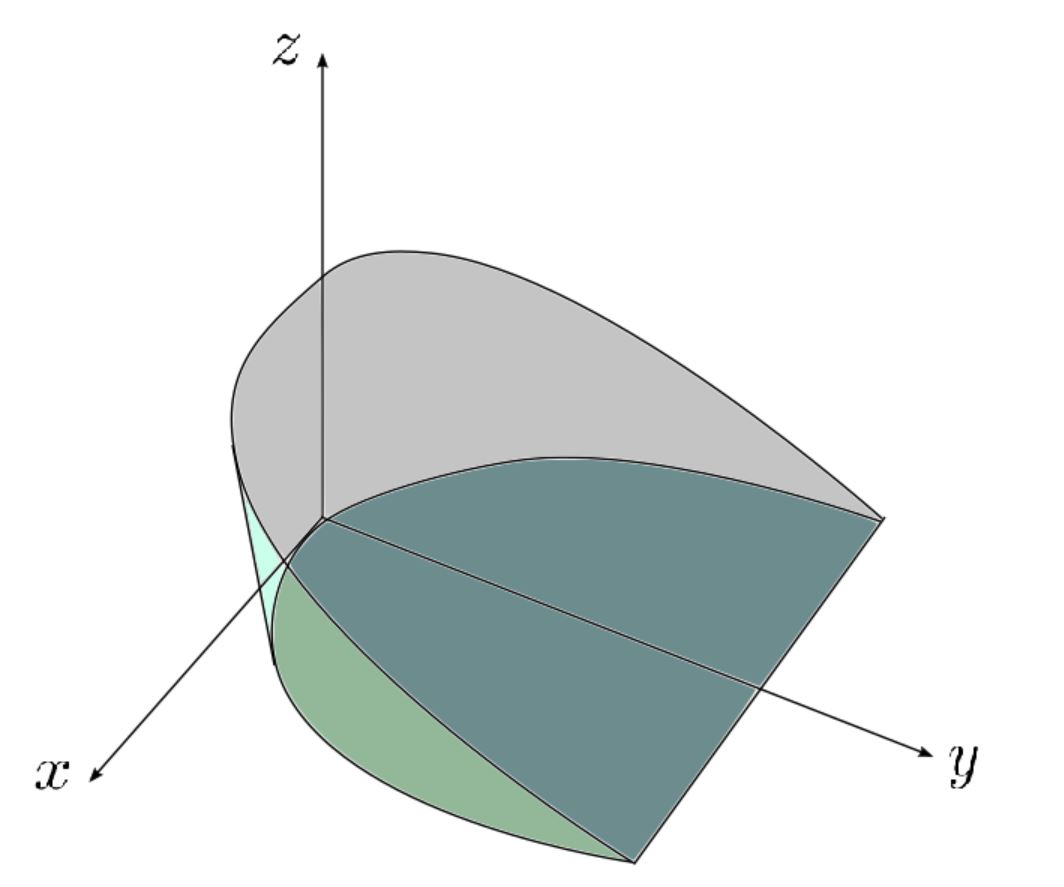
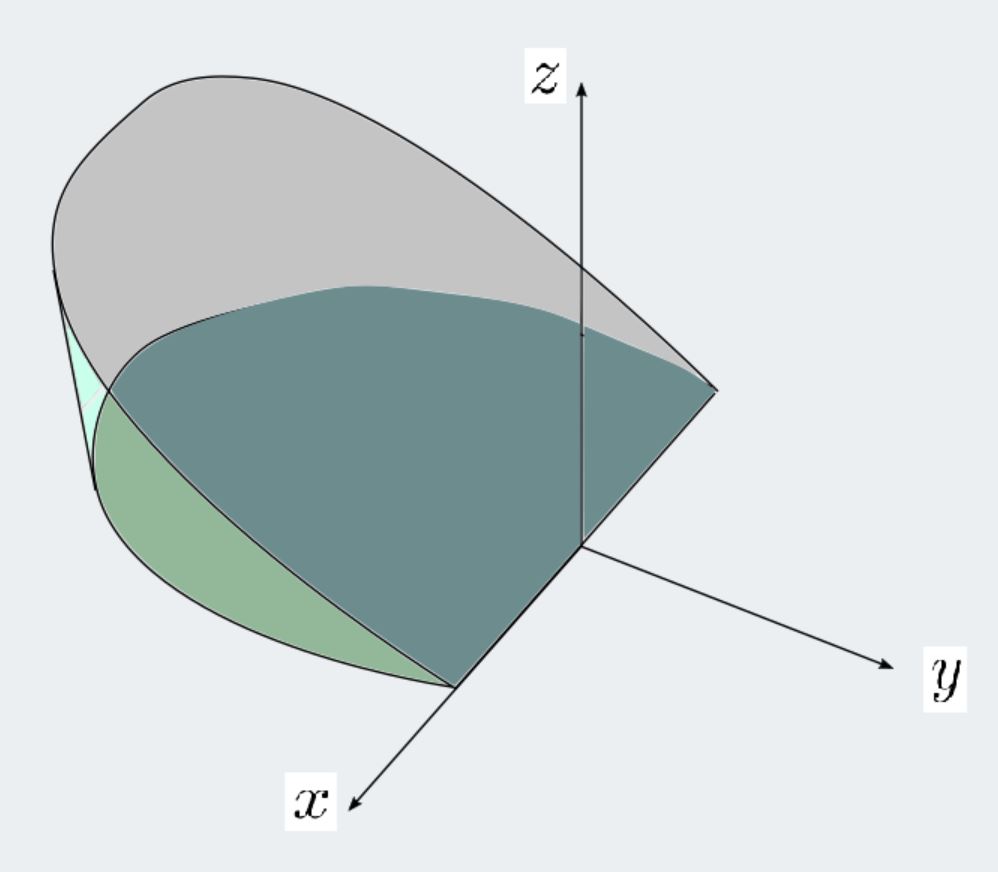
Find the volume of the solid in the first octant formed when the cylinder $z=\sin y$ for $0≤y≤π$ is sliced by the planes $y=x$ and $x=0$.

Solution

Note that $D={(x,y,z)\ :\ 0 \leq x \leq y,\ 0 \leq y \leq \pi,\ 0 \leq z \leq \sin y}.$

The volume, then, is given by $\begin{aligned} V &= \int_0^\pi \int_0^y \int_0^{\sin y} \ dz\ dx\ dy\ &= \int_0^\pi \int_0^y \sin y\ dx\ dy\ &= \int_0^\pi y \sin y\ dy\ &= -y\cos y + \sin y \bigg|_0^\pi \ \ \ \textrm{ (using Integration by Parts)}\ &= \ans{\pi} \end{aligned}$

Find the volume of the prism in the first octant bounded by $z=2−4x$ and $y=8$.

Solution

Note that $D={(x,y,z)\ :\ 0 \leq x \leq 1/2,\ 0 \leq y \leq 8,\ 0 \leq z \leq 2-4x}.$

The volume, then, is given by $\begin{aligned} V &= \int_0^8 \int_0^{1/2} \int_0^{2-4x} \ dz\ dx\ dy\ &= \int_0^8 \int_0^{1/2} 2-4x\ dx\ dy\ &= \int_0^8 \bigg[ 2x-2x^2 \bigg]_0^{1/2}\ dy\ &= \int_0^8 \dfrac{1}{2}\ dy = \ans{4} \end{aligned}$

Find the volume of the wedge bounded by the parabolic cylinder $y=x^2$ and the planes $z=3−y$ and $z=0$.

Solution

Note that $D={(x,y,z)\ :\ -\sqrt{3} \leq x \leq \sqrt{3},\ x^2 \leq y \leq 3,\ 0 \leq z \leq 3-y}.$

The volume, then, is given by $\begin{aligned} V &= \int_{-\sqrt{3}}^{\sqrt{3}} \int_{x^2}^{3} \int_0^{3-y} \ dz\ dy\ dx\ &= \int_{-\sqrt{3}}^{\sqrt{3}} \int_{x^2}^{3} 3-y\ dy\ dx\ &= \int_{-\sqrt{3}}^{\sqrt{3}} \dfrac{9}{2}-3x^2+\dfrac{1}{2}x^4\ dx\ &= \dfrac{9}{2}x-x^3+\dfrac{1}{10}x^5 \bigg|_{-\sqrt{3}}^{\sqrt{3}} = \ans{\dfrac{24\sqrt{3}}{5}} \end{aligned}$