Volumes by Slicing

General Volumes

We'll approach the problem of finding volumes the same way we did areas:

  1. Slice
  2. Approximate
  3. Integrate

Take a look at the picture below to see this process.

General volume picture

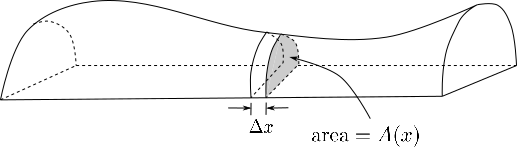
If we cut this entire volume into small slices (like a loaf of bread), we can make an approximation by assuming that the cross-sectional area is consistent across each slice. Then the volume of the slice is A(x)⋅ΔxA(x) \cdot \Delta x just like the volume of a cylinder is the area of the base times the height.

The approximate volume of the entire object will be the sum of the volumes of these slices: V≈∑i=1nA(x) ΔxV \approx \sum_{i=1}^n A(x) \ \Delta x

Finally, by letting the slices become infinitesimally thin, we get the exact volume: V=∫abA(x) dx\ans{V = \int_a^b A(x) \ dx}

Thus, the main question in each problem is to find A(x)A(x), the cross-sectional area as a function of xx.

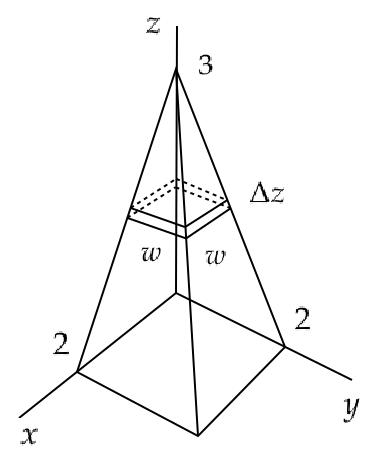
Find the volume of the solid shown below.

alt text

Solution

If we slice this object as shown, the cross sections will all be squares; the length of the sides ww will vary with zz. The integral will be in terms of zz, and the volume will be V=∫02A(z) dz=∫02(w(z))2 dz\begin{aligned} V &= \int_0^2 A(z) \ dz\ &= \int_0^2 (w(z))^2\ dz \end{aligned}

All that remains, then, is to find an expression for ww in terms of zz; there are several ways to do this, but I'll show an algebraic method for it.

Find w(z)w(z)

Look at the values of zz where we know what ww is:

As you can see in the picture, ww is a linear function of zz, so all we need to do is find the equation of the line that connects these two points:

Thus, w=−23z+2w = -\dfrac{2}{3}z + 2

Putting it all together

V=∫03(−23z+2)2 dz=∫0349z2−83z+4 dz=427z3−43z2+4z∣03=4−12+12=4 units2\begin{aligned} V &= \int_0^3 \left(-\dfrac{2}{3}z+2\right)^2\ dz\ &= \int_0^3 \dfrac{4}{9}z^2 - \dfrac{8}{3}z + 4\ dz\ &= \dfrac{4}{27}z^3 - \dfrac{4}{3}z^2 + 4z \bigg|_0^3\ &= 4 - 12 + 12\ &= \ans{4 \textrm{ units}^2} \end{aligned}

  1. Let RR be the region in the first quadrant bounded by the coordinate axes and y=1−x2y=1-x^2. A solid has base RR, and cross sections through the solid perpendicular to the base and parallel to the yy-axis are squares. Find the volume of this solid.

    2. V=∫A(x) dxA(x)=(1−x2)2V=∫01(1−x2)2 dx=∫011−2x2+x4 dx=x−23x3+15x5∣01=815\begin{aligned} V &= \int A(x)\ dx\ A(x) &= (1-x^2)^2\ V &= \int_0^1 (1-x^2)^2\ dx\ &= \int_0^1 1-2x^2+x^4\ dx\ &= x - \dfrac{2}{3}x^3 + \dfrac{1}{5}x^5 \bigg|_0^1\ &= \ans{\dfrac{8}{15}} \end{aligned}

Rotationally Symmetric Objects

There's one whole class of problems where the object looks like the picture below.

Rotationally symmetric object

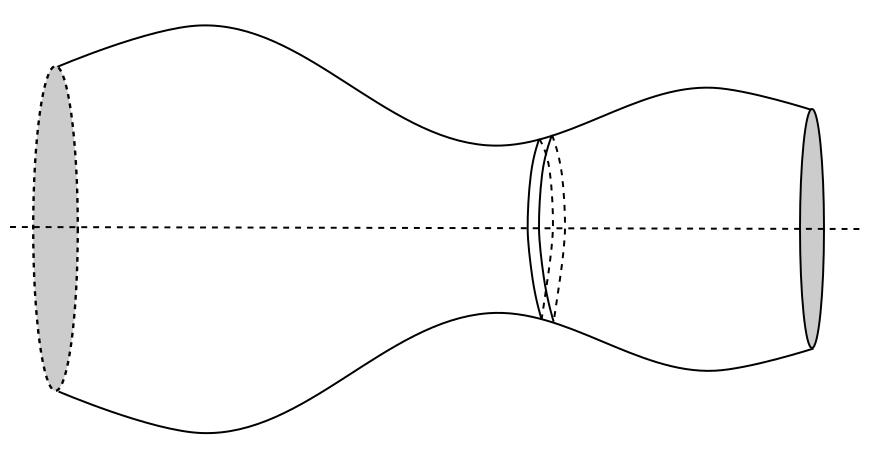
Think about a bowling pin or a baseball bat, or anything that could be made using a lathe, as in the picture below.

Lathe

The nice thing is that the cross-sectional areas will all be circles; thus, all we have to find is the radius. If you look back at the first picture, you can see that the radius is the distance from the centerline to the outer edge, generally defined by a function in the examples we'll do.

Disks

If the object is solid all the way through, the slices will be solid disks, like the one shown below.

Generic Disk

Then the cross-sectional area function will be A(x)=πr2A(x) = \pi r^2 so the volume will be V=π∫abr2 dxV = \pi \int_a^b r^2 \ dx and the problem will be to find rr as a function of xx.

Washers

There are some objects that are not solid all the way through, but have a hollow in the middle. The slices in this case will be washers, like this:

Generic Washer

To find the cross-sectional area of a washer, subtract the missing area in the middle from the area of the outer area. If rr is the inner radius and RR is the outer radius, the area function will be A(x)=πR2−πr2A(x) = \pi R^2 - \pi r^2 so the volume will be V=π∫abR2−r2 dx.V = \pi \int_a^b R^2 - r^2 \ dx.

Disks

Revolve y=xy=x around the xx-axis between x=0x=0 and x=2x=2, and find the volume of the resulting solid.

Revolve y=x around the x-axis

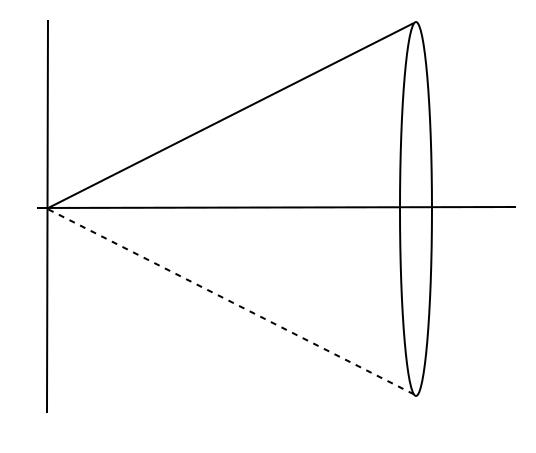
Solution

As we slice up this solid, the cross sections will be disks, and the radii will depend on the curve y=xy=x. At each xx value, the radius will be the corresponding yy value (which just happens to be xx in this case). r=xA(x)=πr2=πx2V=π∫02x2 dx=π3x3∣02=8π3\begin{aligned} r &= x\ A(x) &= \pi r^2\ &= \pi x^2\ V &= \pi \int_0^2 x^2\ dx\ &= \dfrac{\pi}{3}x^3 \bigg|_0^2\ &= \ans{\dfrac{8\pi}{3}} \end{aligned}

  1. Revolve the region bounded by y=1−x2y=1-x^2 and y=0y=0 around the xx-axis, and find the volume of the resulting solid.

    2. r=1−x2A(x)=π(1−x2)2V=π∫−111−2x2+x4 dx=16π15\begin{aligned} r &= 1-x^2\ A(x) &= \pi (1-x^2)^2\ V &= \pi \int_{-1}^1 1-2x^2+x^4\ dx\ &= \ans{\dfrac{16\pi}{15}} \end{aligned}

Washers

Revolve the region bounded by y=2−12xy=2-\dfrac{1}{2}x, y=1y=1, x=1x=1, and x=2x=2 around the xx-axis, and find the volume of the resulting solid.

First washer example

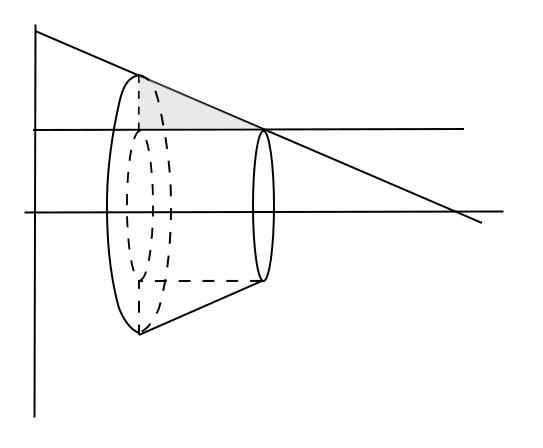
Solution

This solid is hollowed out in the middle, so the slices will be washers instead of disks.

The washers have two radii, the inner radius and outer radius. The inner radius will be defined by the curve that is closer to the center of rotation (y=1y=1), and the outer radius will be defined by the other curve. R=2−12xr=1A(x)=πR2−πr2=π(2−12x)2−π(1)2=π(3−2x+14x2)V=π∫123−2x+14x2 dx=π[3x−x2+112x3]12=π[(6−4+812)−(3−1+112)]=7π12\begin{aligned} R &= 2-\dfrac{1}{2}x\ r &= 1\ A(x) &= \pi R^2 - \pi r^2\ &= \pi\left(2-\dfrac{1}{2}x\right)^2 - \pi(1)^2\ &= \pi \left(3-2x+\dfrac{1}{4}x^2\right)\ V &= \pi \int_1^2 3-2x+\dfrac{1}{4}x^2\ dx\ &= \pi \left[3x-x^2+\dfrac{1}{12}x^3\right]_1^2\ &= \pi\left[\left(6-4+\dfrac{8}{12}\right) - \left(3-1+\dfrac{1}{12}\right)\right]\ &= \ans{\dfrac{7\pi}{12}} \end{aligned}

  1. Revolve the region bounded by y=xy=x and y=x2y=x^2 around the yy-axis, and find the volume of the resulting solid.

    2. R=yr=yA(y)=π(y−y2)V=π∫01y−y2 dy=π6\begin{aligned} R &= \sqrt{y}\ r &= y\ A(y) &= \pi(y-y^2)\ V &= \pi \int_0^1 y-y^2\ dy\ &= \ans{\dfrac{\pi}{6}} \end{aligned}

So far, all of these examples have involved revolving some region around either the xx- or yy-axis, but we can also revolve around some other vertical or horizontal line.

Revolving Around Arbritrary Line

Revolve the region bounded by x=y2x=y^2 and x=1x=1 around the line x=−1x=-1, and find the volume of the resulting solid.

Second washer example

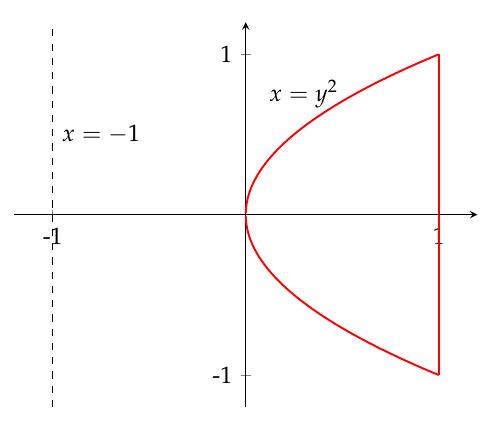
Solution

As we slice this, we'll end up with horizontal washers, with thickness Δy\Delta y. The outer radius will be based on the line x=1x=1: it will be the distance between that and the center of rotation: x=−1x=-1: R=1−(−1)=2R = 1 - (-1) = 2

Similarly, the inner radius will be the distance between x=y2x=y^2 and x=−1x=-1: r=y2−(−1)=y2+1r = y^2 - (-1) = y^2+1

Thus the cross-sectional area function will be A(y)=π(R2−r2)=π(4−(y2+1)2)=π(−y4−2y2+3)\begin{aligned} A(y) &= \pi (R^2 - r^2)\ &= \pi (4-(y^2+1)^2)\ &= \pi (-y^4-2y^2+3) \end{aligned} and the volume will be V=π∫−11−y4−2y2+3 dy=π[−15y5−23y3+3y]−11=64π15\begin{aligned} V &= \pi \int_{-1}^1 -y^4 - 2y^2 + 3\ dy\ &= \pi \left[-\dfrac{1}{5}y^5 - \dfrac{2}{3}y^3 + 3y\right]_{-1}^1\ &= \ans{\dfrac{64\pi}{15}} \end{aligned}

  1. Revolve the region bounded by y=xy=x and y=x2y=x^2 around the line x=2x=2, and find the volume of the resulting solid.

    2. R=y−2r=y−2A(y)=π[(y−2)2−(y−2)2]V=π∫01y2−5y+4y dy=π2\begin{aligned} R &= y-2\ r &= \sqrt{y}-2\ A(y) &= \pi\left[(y-2)^2-(\sqrt{y}-2)^2\right]\ V &= \pi \int_0^1 y^2-5y+4\sqrt{y}\ dy\ &= \ans{\dfrac{\pi}{2}} \end{aligned}